|
正規化・座標変換手法
イメージデータまたは、ベクターデータを正規化する時に設定する[正規化・座標変換 手法]について解説します。
- ■ 正規化手法について
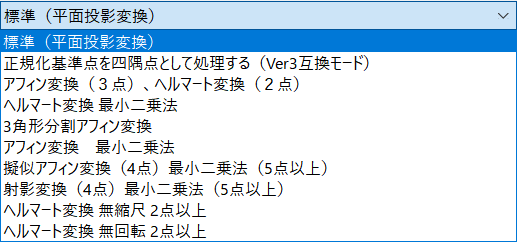
| 基準点個数 | PC-MAPPINGでの変換方法 | 主な処理内容 |
|---|
| n=2 | ヘルマート変換 | 移動・回転・縮尺 |
| n≧3 | ヘルマート変換 最小二乗法 (*1) |
| n=3 | アフィン変換 | スキュー歪・縮尺・移動 |
| n≧4 | アフィン変換 最小二乗法 (*1) |
| n=4 (*2) | 標準(平面投影変換)
正規化基準点を四隅点として処理する(Ver.3互換モード)
疑似アフィン変換(4点)
射影変換(4点) | |
(*1) ヘルマート変換の場合は3点以上の点から、アフィン変換の場合は4点以上の点からそれぞれパラメーターを最小二乗法で求めます。
また、最小二乗法の場合は、オプションの「重みつきで最小二乗法」が利用できます。
(*2) 正規化手法において、
- 標準(平面投影変換)
- 正規化基準点を四隅点として処理する(Ver3互換モード)
- 疑似アフィン変換(4点)
- 射影変換(4点)
は、正規化基準点4点のみが有効で、補助基準点は(追加しても)実際の変換処理では参照されません。
- 標準(平面投影変換)
正規化基準点を四隅点として処理する(Ver.3互換モード)
- 基本的に図郭を押さえてこれを長方形にする変換処理で、逆にいえば、本来、長方形だったものが現状の形になっている問題を数学的にはベクターの各座標点について、2次の方程式を解く方法で「本来の」座標を求めています(PC-MAPPINGではこれを「正規化」処理と呼んでいました)。
-----
平面投影変換
u = (x*a + y*b + c) / (x*g + y*h + 1)
v = (x*d + y*e + f) / (x*g + y*h + 1)
であり、変換係数(a,b,c,d,e,f,g,h)の算出には、最低8個の変換式が必要になり、4つの対応点があれば8個の変換式(X,Yそれぞれ4つ)を生成できます。
よって、4点の正規化基準点が参照されます。
-----
これに対して、
- アフィン変換
- X = ax + by + c
Y = dx + ey + f
- ヘルマート変換(一次等角変換)…アフィン変換の特殊な場合の1つ
- X = ax + by + c
Y = -bx + ay + d
は、ある座標(x,y)を1次(線形)写像で別の座標(X,Y)に変換する「幾何補正」といえます。
式を見れば、アフィン変換は6つ(a,b,c,d,e,f)、ヘルマート変換は4つ(a,b,c,d)のパラメーターを持ち、すなわち、前者は3点(6個の1次方程式)、後者は2点(4個の1次方程式)でパラメーターを決定できます。
特にヘルマート変換においては、変換は移動・回転・伸縮の組み合わせだけで、
- 縮尺 m = (a2 + b2)1/2
- 回転角 θ= tan-1(b/a)
が決定されます。
これらの性格を考えれば、スキャナー取りされた画像のような変形があるもの、地形図のように厳密には不等辺四角形を方眼の経緯度座標系にする場合などを始めとして、多くの場合は(本来の)「正規化」手法(=標準(平面投影法)・正規化基準点を四隅点として処理する(Ver.3互換モード))によって正規化する事が望ましいでしょう。

これに対して、一旦でき上がっている図面の座標変換、すなわち、任意(ペーパー)座標系のデータを公共座標に変換する、斜方眼を正方眼にするなどに対しては基準点数が4点取れない場合、基準点が2点・3点でも実行できるアフィン・ヘルマート変換は有効です。
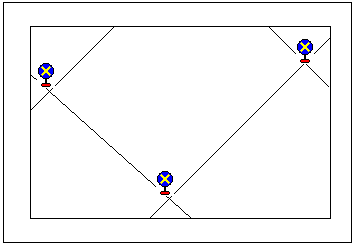
- ■ 基準点の置き方
- 同じ数の基準点であっても、その位置によって正規化の結果が異なります。
- 例えば、4点を用いた「標準」の正規化を行なうとします。
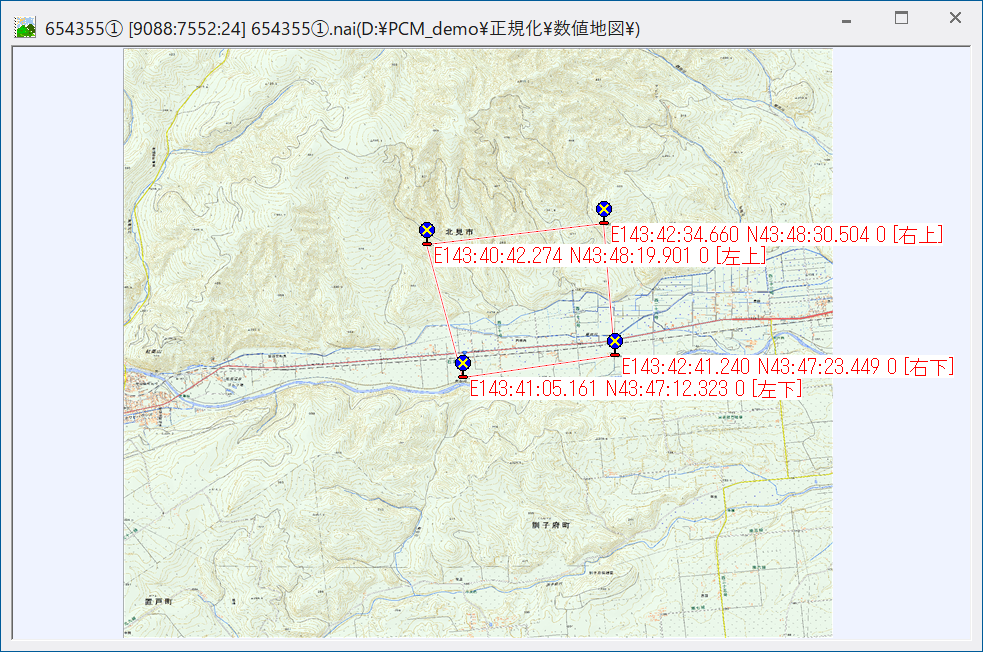
【例①】
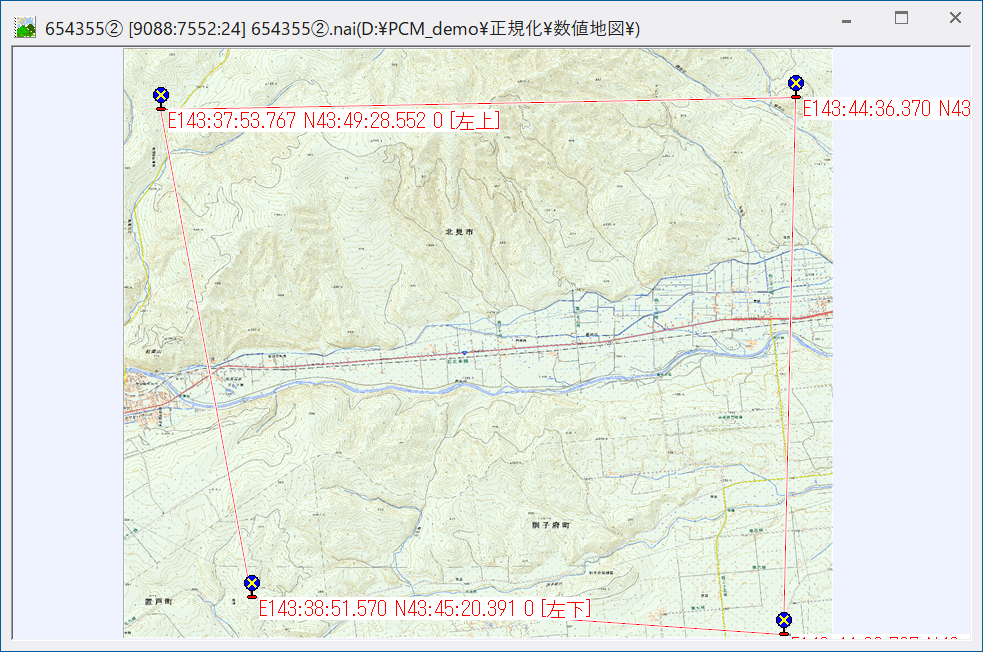
【例②】
- 正規化を実行します。
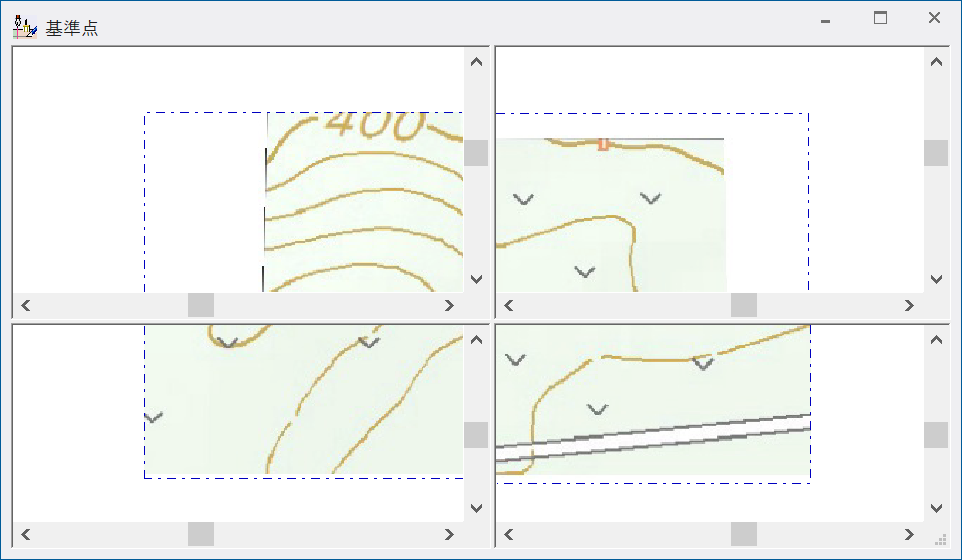
【例①を正規化した結果】:②の結果と比べ、基準点から遠いほど歪みも大きくなります
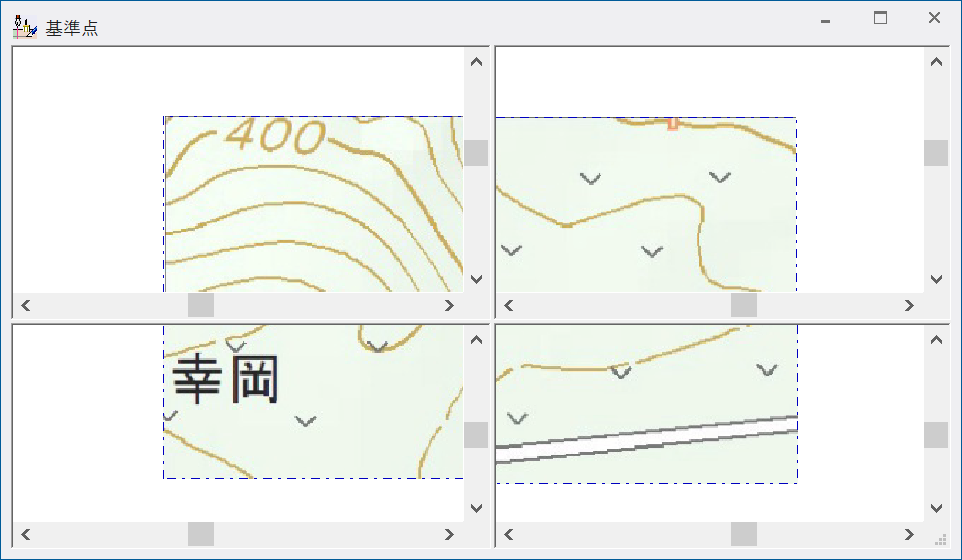
【例②を正規化した結果】
|
















